Знакомство с Monero (часть 2). Адреса-невидимки (stealth-addresses)

Это вторая часть из серии статей по Monero, с её объёмом я тоже ещё не определился. Точку в ней я поставлю, как только почувствую что уже пора это сделать. Первая часть находится здесь.
Во второй части речь пойдёт об адресах-невидимках (stealth-addresses), которые являются существенной частью протокола Monero.
Примечание: работа криптовалюты Monero основана на протоколе Cryptonote, несмотря на то, что это расходилось и продолжает расходиться с многочисленными другими валютами; большая часть этой серии статей будет одинаково хорошо применима с другими частями с некоторыми оговорками. Monero – это просто огромнейший и наиболее активный, основанный на Cryptonote проект.
Здравствуйте! Я вернулся со второй частью моей серии статей по криптографии и приватности Monero. В этой части статьи все понятия я попытаюсь преподнести в максимально простом для понимания виде. Хотелось бы, чтобы «лампочка» внезапного озарения в ваших головах зажигалась в те же моменты, что и у меня, когда я впервые «догнал» эти понятия (мое понимание развивалось на протяжении определенного периода времени).
Во второй части мы будем обсуждать адреса-невидимки (stealth-addresses), также, по ходу дела, вы можете самостоятельно изучить информацию о некоторых новых концепциях.
Адреса-невидимки являются одним из двух дополняющих друг друга методов, обеспечивающих конфиденциальность транзакций для отправителя / получателя в Monero.
Если своими словами, то скрытая адресация – это метод, посредством которого отправитель может принять публичный адрес получателя и преобразовать его в одноразовый адрес таким образом, что:
- Публично невозможно установить происхождение первоначального публичного адреса;
- Публично невозможно установить связь с любым другим адресом, с которым осуществлялось взаимодействие;
- Только получатель может связать вместе все свои платежи;
- Только получатель может получить секретный ключ, связанный с одноразовым адресом.
Используя stealth-адресацию, получатель может опубликовать один адрес и получать на него неограниченное количество* публичных платежей, отследить которые будет невозможно.
*Вероятность коллизии (того, что два stealth-адреса окажутся одинаковыми) криптографически незначительна. Используя Парадокс дней рождения такую вероятность грубо можно было бы выразить как sqrt(l), или, другими словами, должно быть создано приблизительно 2126 stealth-адресов прежде, чем возникнет 50% вероятность конфликтной ситуации. Результатом будет то, что столкнувшиеся адреса станут публично связаны друг с другом и при этом никак не будут связаны с какими-либо другими адресами.
Существует ещё одна, более серьёзная проблема, которая будет происходить в Monero, если столкнутся два одинаковых stealth-адреса, об этом будет рассказано в статье о кольцевой подписи.
Для аналогии, чтобы понять насколько это большая величина 2126, представьте себе картину. Население нашей планеты – 10 миллиардов человек. Каждый человек отправляет платёж каждому другому человеку один раз в секунду. В таком случае числа платежей 2126 мы бы достигли примерно через 27 миллиардов лет.
Stealth-адреса могут быть реализованы в любой другой криптовалюте, в том числе в Bitcoin, но сами по себе они не обеспечивают значительной дополнительной приватности, так как не исключают повторного использования адресов. Тем не менее, они очень удобны для определенных целей, например, если вам необходимо опубликовать адрес для приёма пожертвований, когда его повторное использование будет в основном неизбежно.
Прежде чем понять специфику stealth-адресов в Monero, нам сначала необходимо кое-что обсудить.
Протокол Диффи — Хеллмана на эллиптических кривых (ECDH)
Протокол Диффи - Хеллмана на эллиптических кривых представляет собой вариант оригинального протокола Диффи-Хеллмана. Проще говоря, обе стороны могут самостоятельно сформировать общий секретный ключ, используя незащищенное соединение (при этом подразумевается, что ни один наблюдатель не сможет разгадать этот ключ, просто наблюдая за их связью).
Основы ECDH достаточно просты для понимания, если воспользоваться для этого методом скалярного умножения, о котором я писал в предыдущей статье. Для упрощения все ключевые пары далее будут употребляться строчными / заглавными буквами (приватный ключ а, соответствующий ему публичный ключ A и т.д.).
Представим, что существует некая Алиса. Алиса выбрала случайный секретный ключ (скаляр) а из нашей группы [1, l – 1]. Её публичный ключ A = аG.
С другой стороны существует некий Боб. Точно так же, Боб выбирает случайный секретный ключ b. Его публичный ключ при этом B = bG.
Зная, что разрешается объединять точки, Алиса может вычислить точку C = A + B, но это может сделать и любой другой наблюдатель. C является общей точкой и это не секрет.
Вместо того, чтобы, помнить, что А и В являются точками кривой, и что мы можем добавлять точку к себе (скалярное умножение!), Алиса вычисляет точку D = aB. Это выполняется тем же способом, что и вычисление B = bG, но с другой «базовой точкой». При наличии значений точки D и базовой точки B для стороннего человека уже не будет разницы между тем чтобы узнать а или вычислить значения точки А и базы G.
Боб, в свою очередь, также может вычислить D’ = bA (принята с апострофом, чтобы обозначить её как вторую точку, с которой будем "пробовать" выполнять те же действия). Теперь Алиса и Боб имеют общую секретную точку, известную только им! D = D'
В случае, если не понятно, почему D Алисы равна D' Боба, вот пример:
- Используем базовую точку G
- Принимаем a = 3; A = 3G
- Принимаем b = 4; B = 4G
-
а * b = 12
-
D «Алисы» = аB = 3B = 3*4G = 12G
-
D' «Боба» = bA = 4A = 4*3G = 12G
Обратите внимание, что D имеет соответствующий скаляр d (это 12 в приведенном выше примере), чего никто не знает. В данном случае только мы это знаем, так как знаем a и b!
Это не особенно полезная информация, но я её нахожу весьма интересной.
Stealth-адреса
Теперь, когда вы уже знаете о ECDH, перейдем к вопросу о том, как на самом деле работают двойные ключи stealth-адреса.
Опять же из официального документа Cryptonote, мы имеем следующую информацию:
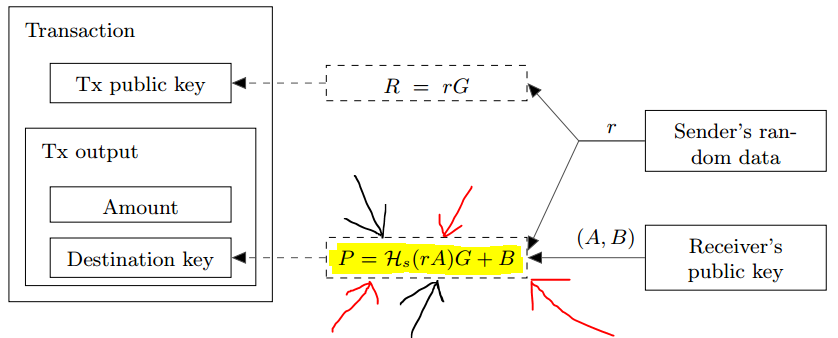
Как я уже подчеркивал и упоминал здесь, мы рассматриваем формулу: P = Hs(rA)G + B.
Двойной ключ относится к паре ключей, отвечающих за расход/просмотр (spend/view keys), которые позволяют выполнять "декодирование" (удаление несвязываемости) stealth-адресов без предоставления одновременного разрешения их траты.
Теперь, давайте забудем всё это и вернёмся немного назад.
Алиса хочет послать компенсацию Бобу. У Алисы есть private spend key -- z и private view key -- у. Её публичный адрес в чётком соответствии с официальным документом в таком случае будет (Z, Y). Я специально использовал буквы, которые не используются выше, потому что ключи Алисы не используются вообще.
Публичный адрес (public address) Боба (А, В). Из предыдущей статьи мы помним, что официальный документ использует А в качестве public view key и B – в качестве public spend key. Предположительно приватными ключами Боба будут (a, b), но Алиса (наш текущий случай) не знает об этом.
В заключение, перед тем, как мы "построим" наш первый stealth-адрес, нам ещё понадобятся величины r и R.
-
r – это новая случайная скалярная величина, которая выбирается Алисой с явной целью создания stealth-адреса для Боба.
-
R – является соответствующей точкой на кривой rG.
Значения r никто не знает и оно может быть уничтожено после использования, если Алиса не захочет позже доказывать третьим лицам, что она произвела оплату Бобу.
R, однако, добавляется к транзакции публично, его значение может видеть каждый. Но для каждой отдельной транзакции должно выбираться новое значение r (повторное использование значения r для отправки к одному и тому же получателю приведет к коллизии stealth-адреса!).
Ниже приведен пример со значением R на chainradar.com:
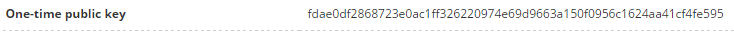
Теперь, когда мы ознакомились с основными определениями по нашей тематике, давайте создадим stealth-адрес! Я считаю, что пошаговое прохождение этого процесса - самый простой способ понять как это работает.
P = Hs(rA)G+B
В соответствии с указанным выше имеем:
-
P - заключительный stealth-адрес (one-time output key, направление, куда будут на самом деле будут отправлены средства);
-
Hs* - алгоритм хэширования, который возвращает скаляр (то есть, выходной хэш интерпретируется как целое и округляется по модулю l);
-
r - новый случайный скаляр, который выбрала Алиса для этой транзакции;
-
A - public view key Боба;
-
G - стандартная Ed25519 базовая точка;
-
B - public spend key Боба.
Примечание: алгоритм хеширования в Monero и других Cryptonote-валют – keccak-256. В данной статье основное внимание сосредоточено не на алгоритмах хеширования, поэтому если хотите узнать больше о них – можете почитать статьи на соответствующую тему. Википедия, однако, по поводу этого алгоритма имеет хороший краткий перечень свойств, который будет нам интересен. Благодаря этому алгоритму:
- Можно быстро вычислить хэш-значение для любого полученного сообщения;
-
Невозможно сгенерировать сообщение из его хэш-значения, кроме как с помощью перебора всех возможных вариантов;
- Даже незначительное изменение в сообщении должно настолько широко менять значение хеш-функции, чтобы это новое значение никоим образом не коррелировало со старым;
- Становится невозможным найти два различных сообщения с одинаковым значением хэш.
По пунктам выше. #1 – это очевидно; #2 – так как сообщение является односторонней собственностью; #3 – очень интересно, так как «не коррелировало» очень похоже на наше волшебное словосочетание «невозможно установить связь». #4 – устойчивость к возникновению коллизий очень важна, так как плохой алгоритм может значительно увеличить шансы на возникновение коллизии со stealth-адресом (см.версию с вероятностью 2126, которая описана выше).
К этому списку я хотел бы добавить такие дополнительные свойства этого алгоритма:
- возможна любая длина на входе;
- фиксированная длина на выходе;
- выход не может быть предугадан или выбран заранее (сопротивление прообраза) - это связано с #2 выше].
Хорошо, так давайте же наконец создадим stealth-адрес!
- Алиса выполняет действия по протоколу ECDH со случайным образом выбранным r и public view key Боба (А), давайте назовем эту точку D. Никто, кроме Алисы или Боба не может вычислить D (см. обсуждение выше по ECDH).
- Алиса использует D для создания нового скаляра, назовём его f. f = Hs(D). Да, я люблю давать вещам имена. Это шаг, который на самом деле приводит к несвязываемости между выходами Боба (вспомните #3 выше -- подробнее об этом позже)!
- Алиса вычисляет F = fG.
- Алиса вычисляет P = F + B (public spend key Боба).
-
P является скрытым значением!
Теперь давайте рассмотрим перспективу Боба:
- Боб получает транзакцию и он хочет проверить, действительно ли она принадлежит ему.
- Боб извлекает R, которое Алиса любезно приложила к транзакции.
- Боб вычисляет D'. Примечание: Боб не знает (пока), что D' равно D. D' = aR.
- Боб вычисляет f' = Hs(D').
- Боб вычисляет F' = f'G.
- Боб вычисляет P' = F' + B.
- Боб проверяет, является ли Р' равным Р, которое включено в назначение транзакции. Если да, то Боб понимает, что эта оплата принадлежит ему и далее делает некоторые дополнительные шаги (см.ниже). Если нет, Боб игнорирует транзакцию.
Некоторые замечания:
- Вычисление D и D' требует наличия секретных данных: либо r (Алисы) или a (Боба). Таким образом, внешние наблюдатели не имеют возможности вернуться к первому шагу Алисы. Кроме того, так как r выбирается случайным образом, даже если наблюдатель подозревает, что Алиса посылает средства на публичный адрес Боба (который наблюдатель знает), то в связи с наличием задачи ECDLP он до сих пор не сможет отследить этот адрес до значения Р, не зная r или а (даже если учтёт значения переменных введённых позже, а именно D и f).
- Нетрудно заметить, что эта схема даёт Алисе только один выход на Боба через r, но с автоматической деноминацией Monero или другой Cryptonote-валюты, которые имеют много выходов за одну транзакцию. Чтобы получить различные stealth-адреса для каждого выхода, Алиса (и Боб) добавляют к величине D "исходящий индекс" (исходящую позицию в транзакции: 0, 1, 2 и т.д.), прежде чем он будет захеширован для создания общего секретного скаляра f. Это я немного разъяснил шаг 2 Алисы относительно несвязываемости. То есть, в то время как для наблюдателей уже не представляется возможным установить происхождение общего секрета D, то после добавления исходящего индекса появляются дополнительные «неограниченные» несвязываемые выходы, которые создаются из одного общего секрета (смотри пункт 3 в разделе о хэш).
- Возвращаясь к концепции двойного ключа, Боб (или тот, кто работает от его имени со знанием параметров а и В) могут "сканировать" и обнаруживать/устанавливать связь с выходами без знания величины b, которая потребуется чтобы фактически провести трату средств с этого выхода. Официальный документ называет (а,B) «ключом отслеживания» (tracking key).
- Возможно выполнить скрытую адресацию не прибегая к методу двойных ключей, но в таком случае придётся пойти на один из двух компромиссов. Вы можете либо: (1). использовать понятие из технической документации под названием truncated address («усечённый адрес»), которое означает, что пара ключей для просмотра публично известна и все входящие транзакции можно отследить (a = Hs(B )); либо: (2). полностью отказаться от пары ключей отвечающих за просмотр (view key pair), что означает, что для сканирования потребуется расшифровка ключей, отвечающих за трату средств (P = Hs(rB)G + B ).
Дополнительные шаги Боба
Итак, Боб определил, что некоторые выходы в транзакции принадлежат ему. Что он будет делать дальше? Я могу представить себе две вещи, которые он хотел бы сделать: проверить, потрачены ли уже средства на этом выходе и (позже) на самом деле потратить эти средства.
Чтобы выполнить любую из этих вещей, Боб должен сначала вычислить секретный ключ (secret key), связанный с этим выходом (one-time secret key, x).
- Боб пересчитывает f' = Hs(D') (как описано выше).
- Боб получает х = f' + b (b – private spend key Боба, отвечающий за трату средств). Что очень здорово, так это то, что P = xG! Объединение скаляров (или точек) вместе сохраняет линейность. P = xG = (f’ + b)G = F' + B
- Для того чтобы проверить потрачено ли Р, Боб вычисляет свой "образ ключа" и запрашивает у блокчейна, из которого видно, помечен ли он как потраченый. Образ ключа I = xHp(P). Более доходчиво это будет описано в статье о кольцевых подписях.
- Для того, чтобы потратить P, Боб должен подписать новую транзакцию с х (подробнее об этом также будет в статье о кольцевых подписях).
[Можете пропустить следующий раздел, если ненавидите "веселье".]
Здесь я буду использовать функции, доступные в Javascript. Это позволит любопытным и проницательным читателем (скорее всего это вы) легко воспроизвести результаты, имея под рукой лишь веб-браузер. Если пойдёте по ссылке выше и откроете консоль браузера (правой кнопкой мыши на странице -> Просмотреть код, затем откроете вкладку Console), то сможете вводить или копировать/вставлять все команды, приведенные ниже, чтобы "увидеть в действии" создание и работу stealth-адреса. Все буквенные обозначения и номера шагов соответствуют приведенным выше.
Скаляры b и r ниже были сгенерированы случайным образом с помощью random_scalar(); (вам, конечно же, не следует в такой же способ генерировать свои собственные скаляры, если вы хотите воспроизвести мои результаты!). Увидеть содержимое переменной можно просто введя её имя и нажав… "//" – так обозначается комментарий в JavaScript.
Вот код взятый из консоли Chrome:

Предварительно
1. var b = "c595161ea20ccd8c692947c2d3ced471e9b13a18b150c881232794e8042bf107"; //private spend key Боба
2. var a = hash_to_scalar(b ) ; //private view key Боба (детерминированная производная) a = "fadf3558b700b88936113be1e5342245bd68a6b1deeb496000c4148ad4b61f02"
3. var B = sec_key_to_pub(b ); //public spend key Боба, эта функция умножает базу G на входящее значение; B = "3bcb82eecc13739b463b386fc1ed991386a046b478bf4864673ca0a229c3cec1"
4. var A = sec_key_to_pub(a); //public view key Боба, A = "6bb8297dc3b54407ac78ffa4efa4afbe5f1806e5e41aa56ae98c2fe53032bb4b"
5. pubkeys_to_string(B,A); //возвращает public address Боба (для любознательных) "43tXwm6UNNvSyMdHU4Jfeg4GRgU7KEVAfHo3B5RrXYMjZMRaowr68y12HSo14wv2qcYqqpG1U5AHrJtBdFHKPDEA9UxK6Hy"
6. var r = "c91ae3053f640fcad393fb6c74ad9f064c25314c8993c5545306154e070b1f0f";
7. var R = sec_key_to_pub(r ); //R = "396fc23bc389046b214087a9522c0fbd673d2f3f00ab9768f35fa52f953fef22"
Алиса
1. var D = generate_key_derivation(A, r); //ECDH, rA; D = "a1d198629fadc698b48f33dc2e280301679ab2c75a76974fd185ba66ab8418cc"
2. var f = derivation_to_scalar(D, 0); //0 -- это внешний индекс; стандартный метод объединяет эти последние несколько шагов в один, но я разделил их для большего понимания; f = "bf1d230a09bfdb0bc7fe04cddf8c1635d0ebaaf159ef85dc408ae60879752509"
3. var F = sec_key_to_pub(f); // F = "3e4b39c5b5110d6fbdb77fbcd203709c19fefd28c982a86bda3f3d35fc099738"
4. var P = ge_add(F,B ); //"ge" – означает групповой элемент; эта функция объединяет две точки вместе. P = "6cabaac48d3b9043525a703e9e5feb72132f69ea6deca9b4acf9228beb74cd8f"
Боб
1. N/A
2. N/A
3. var D1 = generate_key_derivation(R, a); //D1 = тот же, что и выше!
4. var f1 = derivation_to_scalar(D1, 0); //f1 = тот же что и выше!
5. var F1 = sec_key_to_pub(f1); //F1 = тот же что и выше!
6. var P1 = ge_add(F1,B ); //P1 = от же что и выше!
Дополнительные шаги Боба
1. N/A
2. var x = sc_add(f1,b ); //“sc” означает скаляр; эта функция объединяет два скаляра. x = "97df43cb906896405a8b54ecd4610c92b99de5090b404e5e64b17af17da01601". Теперь для интереса введите sec_key_to_pub(x); и сравните с Р
3. var I = generate_key_image_2(P, x); //эта функция объединяет в себе "hash_to_ec" (Hp, хэш точки на кривой) и скалярное умножение новой точки на х. I = "2ba7ee37314d4a1edbeef727f49099c79d55797570cb1206ee2685c94b6550b1" (для забавы -- spent status)
4. N/A
Далее кратко о чём была эта статья.
Скрытая адресация позволяет отправителям создавать от имени получателя "неограниченное" количество одноразовых адресов для отправки транзакций (без какого-либо взаимодействия при этом).
Средства на этих адресах могут быть восстановлены и израсходованы только получателем и не могут быть публично связаны друг с другом, или со стандартным адресом, с которого они были получены.
До новых встреч!
Большое спасибо переводчику за его труд.Также и вы можете сказать "Спасибо", ниже оставляю его просьбу.
У дочери обнаружили нейробластому, 4 стадия с метастазами в шейных лимфоузлах.
Подробности в группах на фейсбуке и вконтакте:
https://www.facebook.com/groups/1862662937341925/
Всех небезразличных прошу помочь.
Мой BTC-кошелек: 1JDLdjTNvkDFmpiXAKuvN4RZNxqnRynsyc
Дополнительные реквизиты указаны в постах по ссылкам.
Спасибо!











0 Комментариев
Рекомендуемые комментарии
Комментариев нет
Для публикации сообщений создайте учётную запись или авторизуйтесь
Вы должны быть пользователем, чтобы оставить комментарий
Создать учетную запись
Зарегистрируйте новую учётную запись в нашем сообществе. Это очень просто!
Регистрация нового пользователяВойти
Уже есть аккаунт? Войти в систему.
Войти